Si el triángulo tiene un ángulo recto (90°), y pones un cuadrado sobre cada uno de sus lados, entonces el cuadrado más grande tiene exactamente la misma área que los otros dos cuadrados juntos.
El lado más largo del triángulo se llama hipotenusa, así que la definición normal es:
-En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los otros 2 lados.
Entonces, el cuadrado de a (a²) más el cuadrado de b (b²) es igual al cuadrado de c (c²):
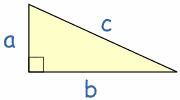 a2 + b2 = c2
a2 + b2 = c2Ejemplo:
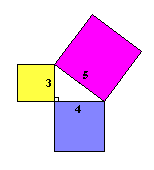
Veamos si las áreas son la misma:
32 + 42 = 52
Calculando obtenemos:
9 + 16 = 25
¡SI, FUNCIONA!





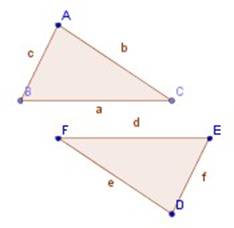



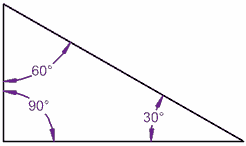 60°+90°+30°= 180°
60°+90°+30°= 180°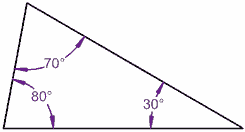 70°+80°+30°= 180°
70°+80°+30°= 180°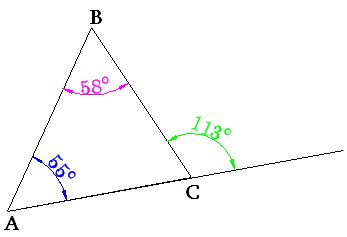

 2.-
2.-
 4.-
4.-
