1.- Relación Seno Coseno
Cos2 a + Sen2 a = 1
2.- Relación Secante Tangente
Sec2 a = 1+ Tag2 a
3.- Relación Cosecante Cotangente
Cosec2 a = 1 + Cotang2 a
Cosec a = 1 / Sen a
Sec a = 1 / Cos a
Cotan a = 1 / Tan a = Cos a / Sen a
Matematicas
sábado, 12 de abril de 2014
Funciones Trigonométricas en el Circulo Unitario
La circunferencia trigonométrica, unitaria o "circulo unitario" es una circunferencia de radio 1, normalmente con su centro en el origen (0,0) se un sistema de coordenadas cartesianas.
Dicha circunferencia se utiliza para poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos. auxiliares.
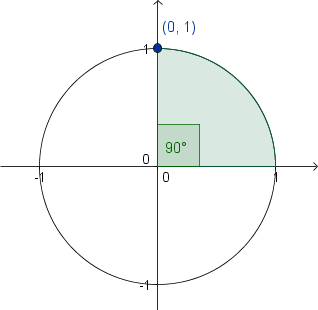
Hay muchas formas de definir localizaciones en el circulo unitario. Vamos a comenzar definiendo una localización (x,y) en el circulo por el ángulo formado entre (x,y) y (0,0) y (1,0).
Dicha circunferencia se utiliza para poder estudiar fácilmente las razones trigonométricas, mediante la representación de triángulos rectángulos. auxiliares.
Hay muchas formas de definir localizaciones en el circulo unitario. Vamos a comenzar definiendo una localización (x,y) en el circulo por el ángulo formado entre (x,y) y (0,0) y (1,0).
La localización (0,1)
se asocia con 90°

Ángulos en la Circunferencia
Ángulo Central:- Su vértice se ubica en el centro, y sus lados son dos radios.

Ángulo Inscrito:- Tiene su vértice esta en la circunferencia y sus lados son secantes a ella. Mide la mitad del arco que abarca.

Ángulo Semi-Inscrito:- El vértice sel ángulo semi-inscrito esta en la circunferencia, un lado secante y otro tangente a ella. Mide la mitad del arco que abarca.

Angulo Interior:- Su vertice es inferior a la circunferencia y sus lados secantes a ella. Mida la mitad de las sumas de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

Ángulo Exterior:- Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son:
o secantes a ella, o uno tangente y otro secante, o tangente a ella.



Ángulo Inscrito:- Tiene su vértice esta en la circunferencia y sus lados son secantes a ella. Mide la mitad del arco que abarca.

Ángulo Semi-Inscrito:- El vértice sel ángulo semi-inscrito esta en la circunferencia, un lado secante y otro tangente a ella. Mide la mitad del arco que abarca.
Angulo Interior:- Su vertice es inferior a la circunferencia y sus lados secantes a ella. Mida la mitad de las sumas de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
Ángulo Exterior:- Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son:
o secantes a ella, o uno tangente y otro secante, o tangente a ella.


Rectas en la Circunferencia

CIRCUNFERENCIA:- Es un lugar geométrico de un conjunto de infinitos puntos que equidistan de un punto citado en el centro.
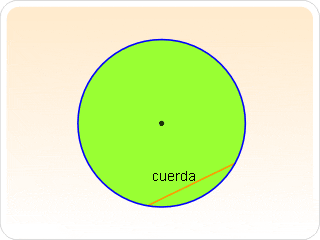 CUERDA:- Es el segmento que une dos puntos de la circunferencia. Las cuerdas tienen distintas medidas.
CUERDA:- Es el segmento que une dos puntos de la circunferencia. Las cuerdas tienen distintas medidas. DIÁMETRO:- Es la cuerda que pasa por el centro de la circunferencia.
DIÁMETRO:- Es la cuerda que pasa por el centro de la circunferencia.Es la cuerda de mayor medida y se nombra con la letra "d". Ademas el diamtre siempre es el doble del radio. d= 2r r= d/2
 ARCO:- Es una parte de la ciercunferencia comprendida entre dos puntos de ella.
ARCO:- Es una parte de la ciercunferencia comprendida entre dos puntos de ella.domingo, 9 de marzo de 2014
Puntos proporcionales
Considera los segmentos AB y CD de la recta r. Se observa que CD = 2 · AB.
¿Qué relación hay entre los segmentos correspondientes A’B’ y C’D’?
Observa que C’D’ es también doble de A’B’:
C’D’ = 2 · A’B’.
Observa también que con estos segmentos se puede escribir esta proporción:
CD / C’D’ = (2 · AB) / (2 · A’B’) = A’B’ / AB.
Esta proporcionalidad existente entre todos los segmentos de la recta r y sus correspondientes de la recta t:
AB / A'B' = AC / A'C' = BC / B'C'=CD / C'D'=k.
AB / A'B' = AC / A'C' = BC / B'C'=CD / C'D'=k.
Si varias paralelas son cortadas por dos rectas secantes, los segmentos que determinan en una de las secantes son proporcionales a los segmentos que determinan en la otra secante.
Áreas y perímetros de figuras geométricas.
Triángulo:
h=Altura b=Base
El triángulo es un polígono formado por 3 lados y tres ángulos, cumpliendo la propiedad de que la suma de todos sus ángulos siempre es 180°.
Área = Base.Altura /2
Perímetro = Lado + lado + lado
Rectángulo:
El rectángulo es un polígono compuesto por dos pares de lados iguales que forman entre si ángulos de 90°.
Área: Base.Altura
Perímetro: lados.2 + lado.2

Cuadrado:
El cuadrado es un polígono formado por cuatro lados de igual longitud que forman entre si ángulos de 90°
Área: (lado.lado)
Perímetro: Lado + lado + lado + lado = 4x lado

Trapecio:
El trapecio es un polígono de cuatro lados, pero sus cuatro ángulos son distintos de 90°.
Área: [(base mayor + base menor)altura] / 2
Perímetro: Suma de todos sus lados.
Rombo:
El rombo es un polígono de 4 lados iguales, pero sus cuatro ángulos son distintos de 90°
Área: (diagonal mayor.diagonal menor) / 2
Perímetro: 4xlado.

Romboide:
Es un polígono de 4 lados los cuales 2 son distinto y los otros 2 también, y todos su ángulos son diferentes a 90°
Área: 2.(altura+base)
Perímetro: 2 x lado + 2 x lado
Pentágono:
El pentágono regular es un polígono de 5 lados iguales y 5 ángulos iguales.
Área: (Perímetro.Apotema) / 2
Perímetro: Suma de todos sus lados

Hexágono:
El hexágono es un polígono de seis lados y seis ángulos iguales.
los ángulos formados, al unir el centro con todos los vértices, son equilateros.
Área: (Perímetro.Apotema) / 2
Perímetro: Suma de todos sus lados
NOTA: Y ASÍ CON TODOS LOS POLÍGONOS REGULARES.
Suscribirse a:
Comentarios (Atom)
